[译]信号系统分析实践——计步器
11th chapter of 500 lines or less in aosabook series.
理想世界与现实世界
在我们的学生时代,我们遇到的大部分问题都是经过精心设计的,在一个理想的情况下发生和解决的问题。
而当我们来到现实世界中的时候,所遇到的问题就会变得复杂的多。
在这一章中,我们就将尝试解决一个这种复杂的现实世界中的问题。
我们将一起构建一个基本的计步器。首先,我们会讨论记不起的原理并设计一套记步器解决方案,然后我们将给出代码实现,最后,我们将增加一个web层来作为用户界面。
计步器的原理
加速度传感器
这个硬件会测量x, y, z三个方向上的加速度。并且我们知道市场上绝大多数智能手机上都有加速度传感器。所以通过加速度来记步,也许是个好选择。
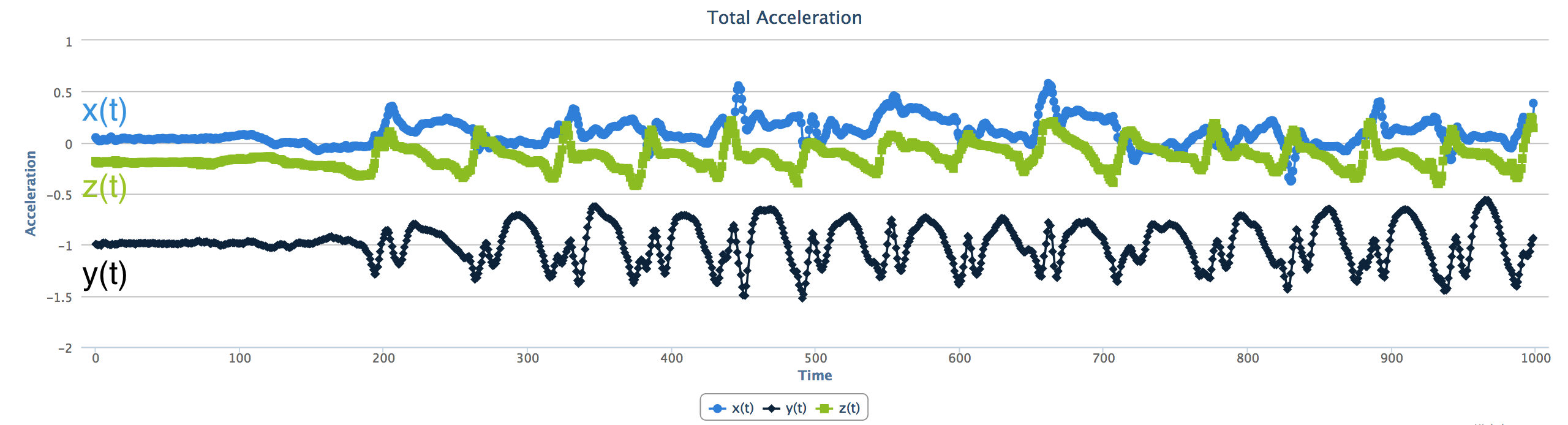
如上图所示,每一个点都代表三维空间中一个方向上的加速度,单位是g,g为9.8m/s^2,是地球表面的平均重力加速度。
走动分析
当人走动的时候,每走一步,身体就会一上一下起伏,不多,可能只有一两厘米,但是这已经是在人类走动过程中,最简单,最清晰,最易识别的加速度信号了。
人每走一步,就会在垂直于地面的方向有一次起伏,或者说与重力加速度相同的方向。
简而言之,我们想要记步,就只要数在重力加速度方向,人每走一步时一上一下起伏,造成的加速度变化即可。
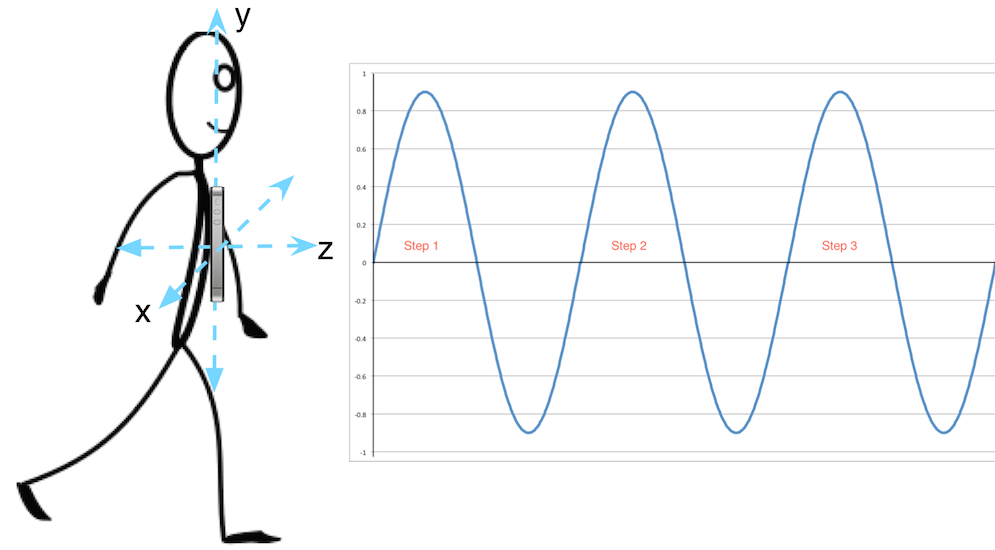
我们对问题进行一些简化,我们假设:
- 我们在向着z轴方向走动
- 每走一步是的起伏在y轴方向
- 在整个走动过程中,手机的方向(加速度传感器x, y, z三轴的方向)不变
那么,走动时的起伏将类似于一个正弦,每一次正弦的起伏都代表人走的一步,记步就变成了数正弦的波峰。
抽象出来的问题解决了,现实世界的问题也不难,无非是更复杂一些罢了,原理都一样。
自然界的力
假设我们的手机平放在桌子上(屏幕朝上),在这个坐标系中,重力加速度在z轴的负方向。如图,即便我们的手机是静止的,加速度传感器依然把重力加速度叠加出来,这很重要,因为重力加速度为我们选定了一个正方向。
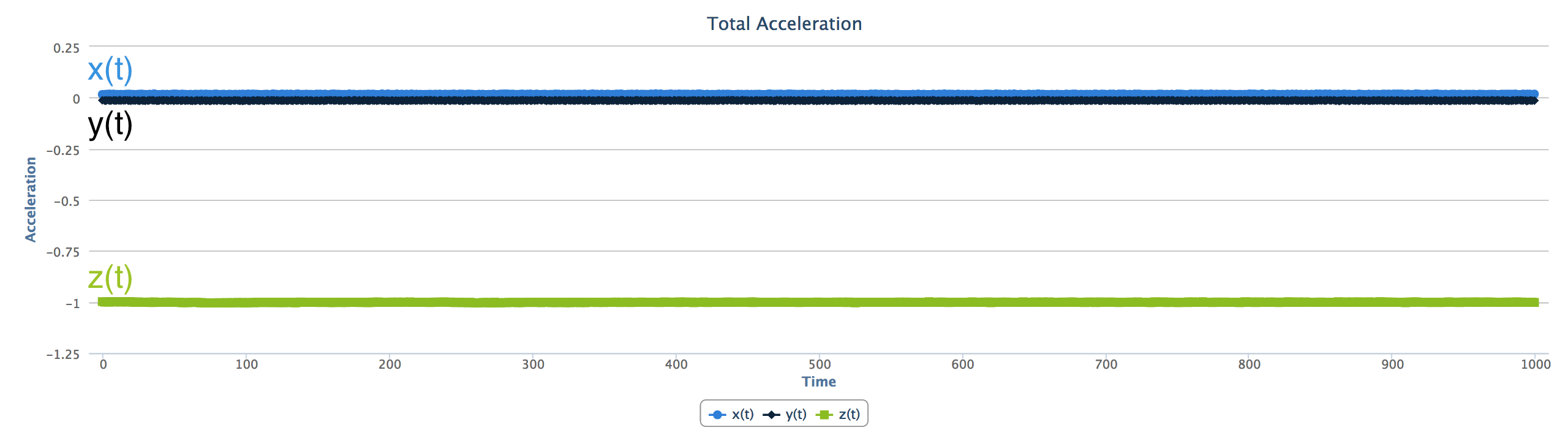
此时,x(t) y(t)都是0 ,而z(t)是常量-1g。
我的意思是,加速度传感器,实际上记录了两种加速度,一种是用户的加速度,一种是重力加速度。
用户加速度,是用户的运动反应到手机上,造成的加速度。如果手机静止的话,加速度就是0。在用户(和手机)一起运动的时候,加速度就很难是0了。
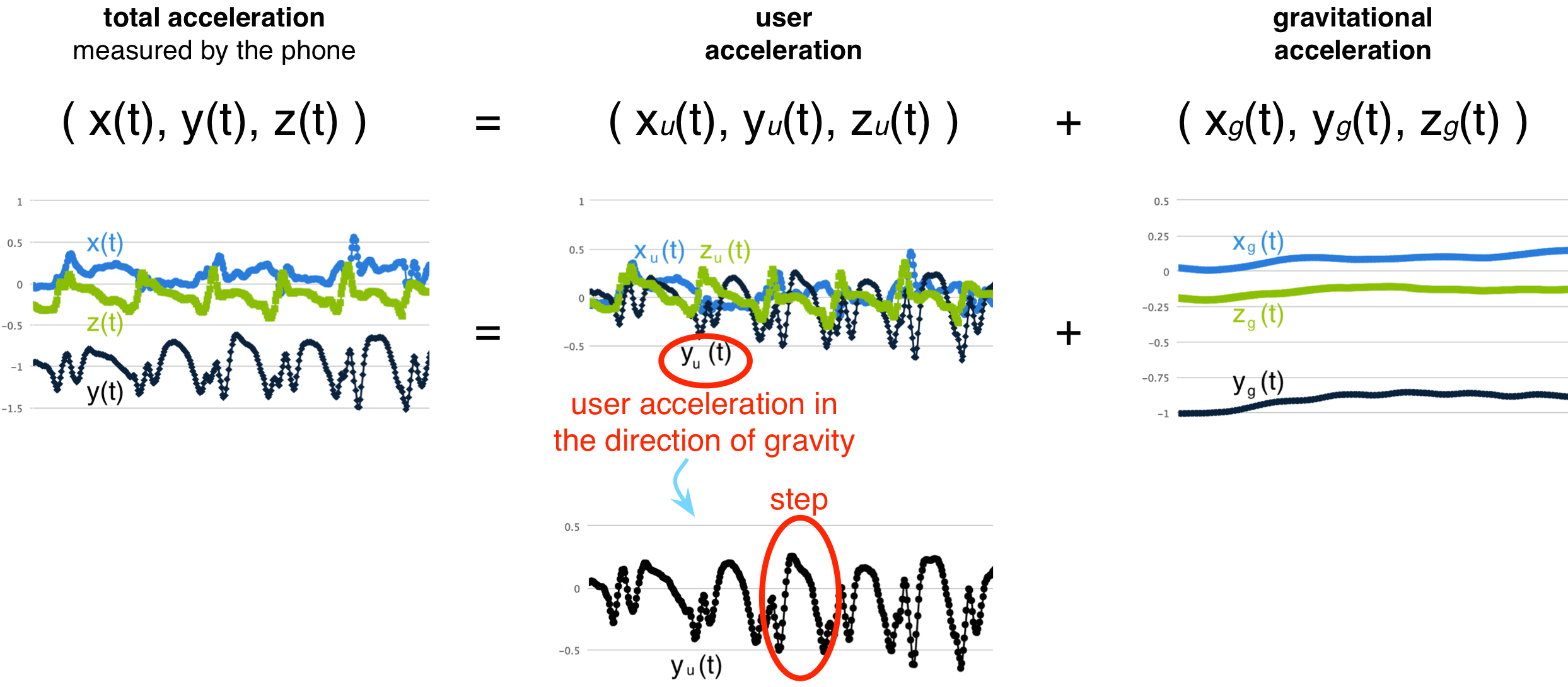
要记步,我们只对在重力加速度方向的用户加速度感兴趣,也就是说我们将只关心x, y, z三个轴上的加速度在重力加速度方向上的分量。如上图所示。
在上面定义的简化模型中,重力加速度在 x(t) z(t)上的分量是0, 在y上的分量是9.8。
所以在总加速度的图中,x,z在0周围波动,y在-1g周围波动。
而在用户加速度的图中,移除重力加速度的影响,三个轴上的信号都会在0周围波动。
ok,那么,我们知道,记步要考虑的就只剩下y轴上的用户加速度了。非常好,接下来,我们将考虑更加实际的情况。
人是复杂的动物
当我们把手机放在口袋里的时候,还好,人和手机基本保持相对静止。但是如果我们把手机放在包里呢,或者一些更加颠簸的位置。
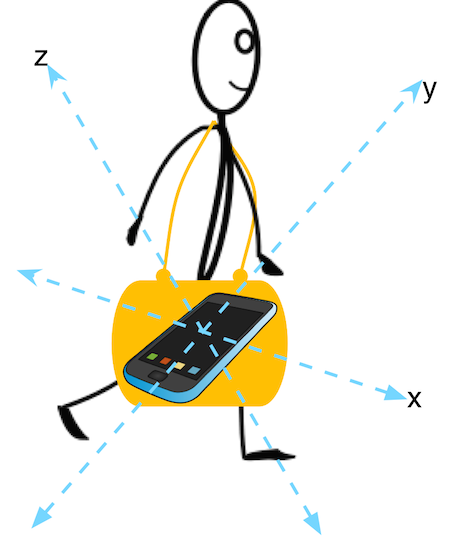
现在重力加速度分布在了x,y,z三个轴上,我们想要知道用户加速度在重力加速度方向上的分量,就需要:
- 把总加速度分解为用户加速度和重力加速度
- 把用户加速度分解,求出在重力加速度方向的分量

1.把总加速度分解为用户加速度和重力加速度
我们可以通过滤波器,来帮助分解
低通滤波与高通滤波
滤波器是用来过滤信号中不需要成分的工具。
低通滤波会只让信号中的低频部分通过,滤去高频部分,高通滤波相反,滤去低频部分。
在我们要解决的问题中,频率(Hz),指的是加速度的变化的快慢程度,(如果真正想要理解,可以搜索一下傅里叶滤波)。一个常量的加速度频率就是0,而不断变化的加速度信号频率就是非0。也就是说重力加速度是一个0Hz的信号,而用户加速度并不。
在每一个轴上,我们都可以对总加速度使用一个低通滤波器,从而只通过重力加速度,然后总价速度减去重力加速度,来得到用户加速度
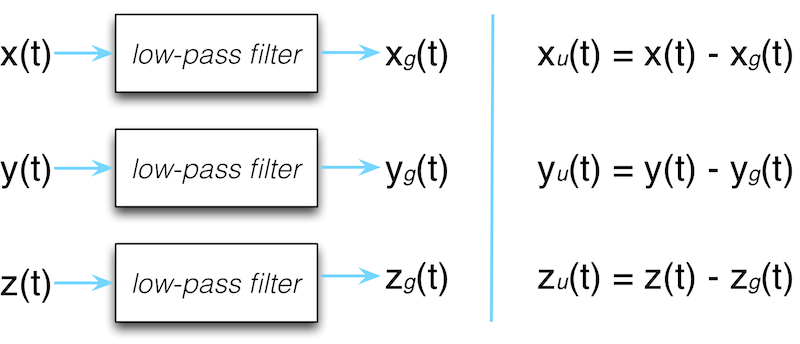
事实上,数学家们设计了许许多多的滤波模型,我们将使用的滤波器被叫做无限冲激响应滤波器(IIR)。
我们选择IIR是因为它好上手,并且易于拓展。我们选择的滤波器通过下式实现。
$$
output{i} = \alpha{0}(input{i}\beta{0} + input{i-1}\beta{1} + input{i-2}\beta{2} - output{i-1}\alpha{1} - output{i-2}\alpha{2})
$$
数字滤波器的原理和设计超出了这一章的讨论范围,但是对它进行一些简单的讨论依然是有必要的。在许多处理实际问题的应用中,滤波器都是非常重要的知识点。数字滤波器,可以滤掉某个频率或者保留某个范围内的频率。$\alpha$和$\beta$是公式的系数,它们标识着将滤去的频率,或者我们想保留的频率范围。
我们希望能够能够滤去除常量的重力加速度之外的所有频率,所以我们选择一个参数,减弱频率超过0.2Hz的波。注意这里不是0Hz,尽管重力加速度的频率确实是0Hz,但是物理世界里,也确实不完美,所以我们需要允许一个细小的偏差。
实现低通滤波器
- $x(t)$ into $x{g}(t)$ and $x{u}(t)$,
- $y(t)$ into $y{g}(t)$ and $y{u}(t)$, and
- $z(t)$ into $z{g}(t)$ and $z{u}(t)$.
我们需要把前两个重力加速度的点初始化为0,这样$y(t-2)$才能有值。
$$x{g}(0) = x{g}(1) = y{g}(0) = y{g}(1) = z{g}(0) = z{g}(1) = 0$$
那么IIR滤波器,对应到我们要解决的问题,应该是这样的。
$$x{g}(t) = \alpha{0}(x(t)\beta{0} + x(t-1)\beta{1} + x(t-2)\beta{2} - x{g}(t-1)\alpha{1} - x{g}(t-2)\alpha_{2})$$
$$y{g}(t) = \alpha{0}(y(t)\beta{0} + y(t-1)\beta{1} + y(t-2)\beta{2} - y{g}(t-1)\alpha{1} - y{g}(t-2)\alpha_{2})$$
$$z{g}(t) = \alpha{0}(z(t)\beta{0} + z(t-1)\beta{1} + z(t-2)\beta{2} - z{g}(t-1)\alpha{1} - z{g}(t-2)\alpha_{2})$$
滤波器的结果应该是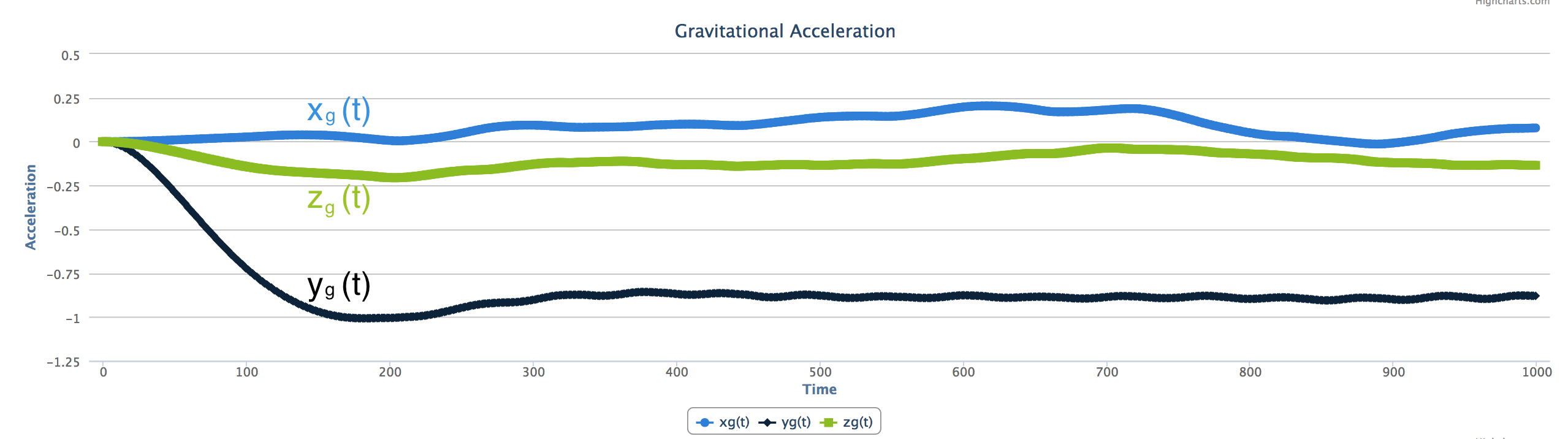
$x{g}(t)$ 和 $z{g}(t)$ 在0周围波动 $y{g}(t)$ 快速落会 $-1g$. $y{g}(t)$开始时的0点是由于公式的初始化。
现在我们通过总加速度减去重力加速度的方式来计算用户加速度。
$$
x{u}(t) = x(t) - x{g}(t)
$$
$$
y{u}(t) = y(t) - y{g}(t)
$$
$$
z{u}(t) = z(t) - z{g}(t)
$$
结果见下图,我们已经成功的将总加速度分解成了用户加速度和重力加速度。
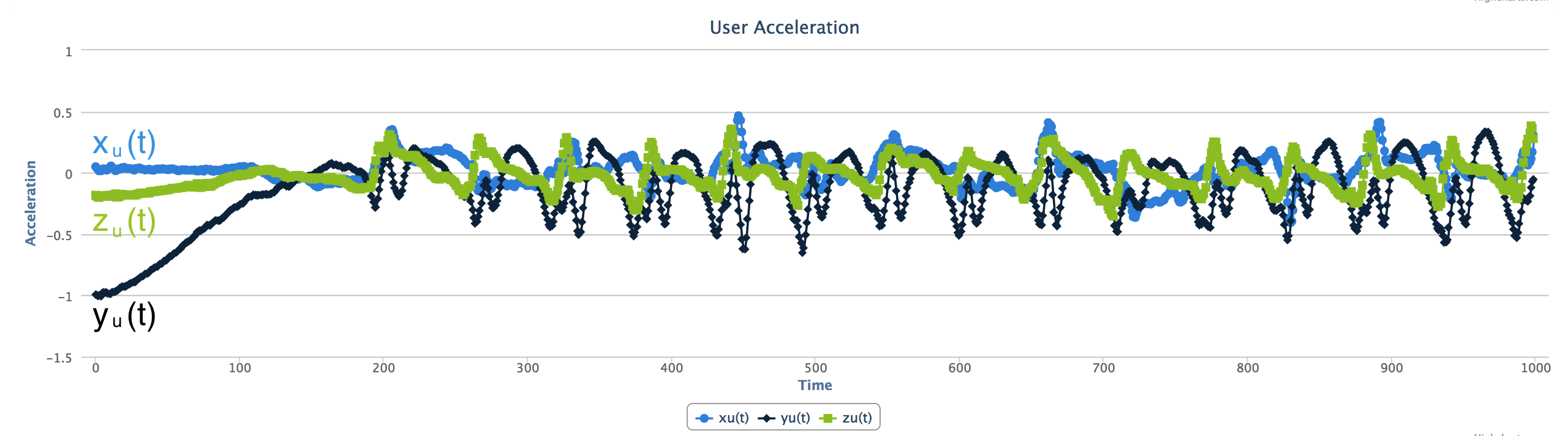
2. 求用户加速度在重力方向上的分量
$x{u}(t)$, $y{u}(t)$, 和 $z_{u}(t)$ 都包括用户的所有动作,而不仅仅是重力方向上的运动。我们现在的目标是将用户加速度分解,并求出用户加速度在重力方向上的加速度。从而将x, y, z三个信号变成了一个。这个信号包含了x, y, z三个轴,每个轴上重力加速度方向上的分量。
好,我们开始!首先,我们需要一些线性代数的知识。
点积
点积,即向量的积。
它可以把两个三维空间的向量变成一个标量。换句话说,他可以把$x(t)$$y(t)$$z(t)$合成到一个维度。
在我们的例子中,我们通过求重力加速度和用户加速度的积的形式,来求得用户加速度在重力加速度方向上的分量。并把它叫做$a(t)$,

使用点积
$$a(t) = x{u}(t)x{g}(t) + y{u}(t)y{g}(t) + z{u}(t)z{g}(t)$$
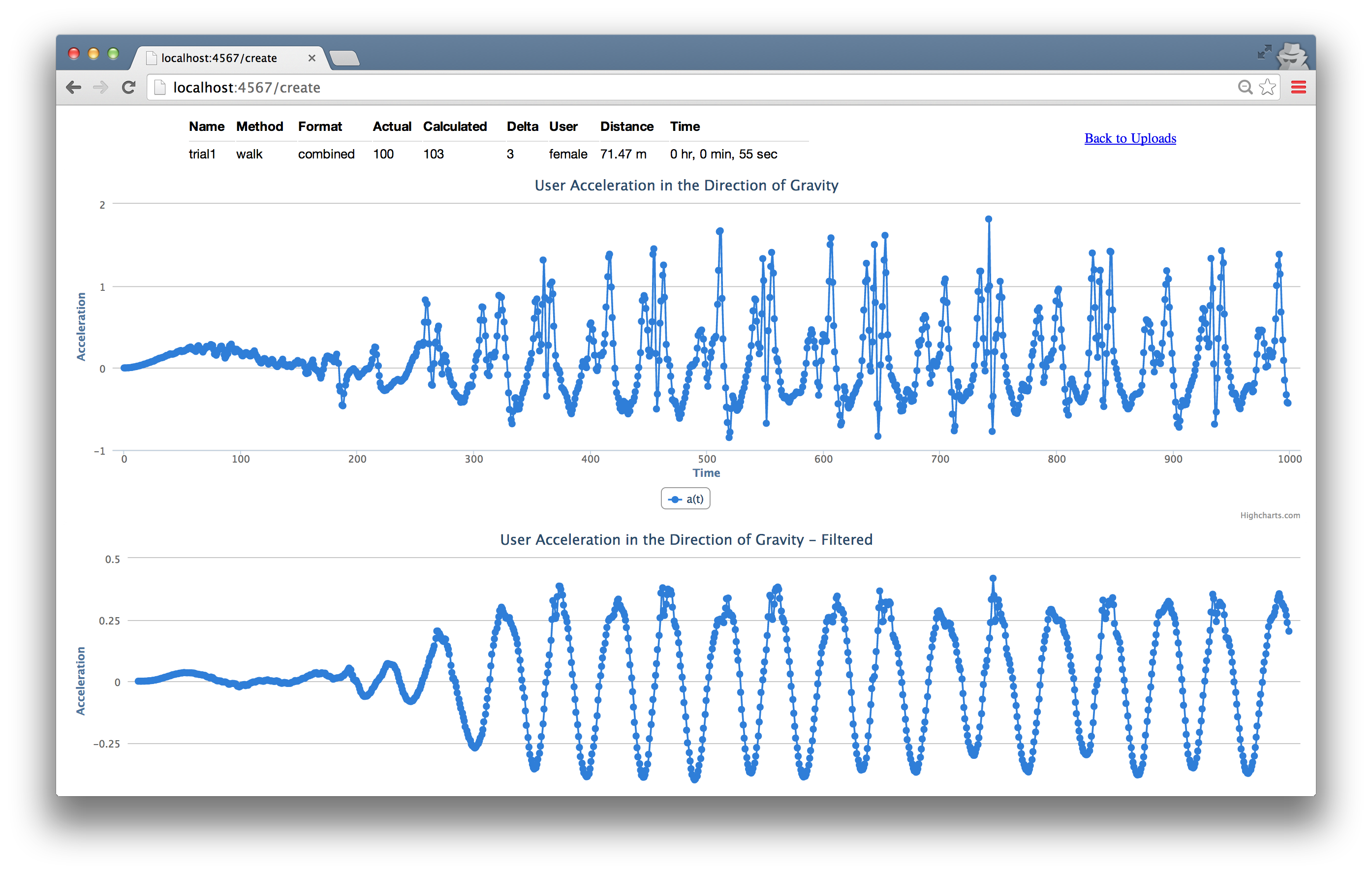
通过上式即可取得用户加速度在重力加速度方向上的分量,得到的$a(t)$如下图。
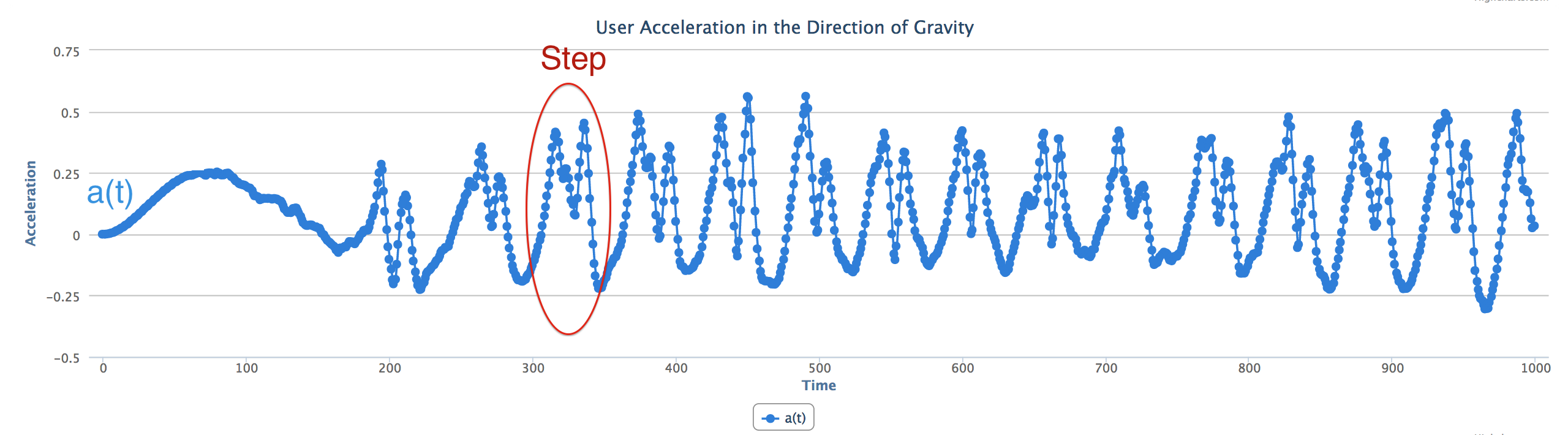
我们现在通过肉眼也可以分辨出哪是一步了。很简单吧。
现实世界的实际情况
任何问题一旦放进现实世界,就会一下子变得特别复杂。但是至少,我们离成功记步已经很近了,至少$a(t)$已经有点像我们预想的sin曲线了。但是,只是有点。我们依然需要让我们得到的$a(t)$曲线更加的平滑。
那么现在我们就需要解决下面四种不平滑的情况。

1. Jumpy Peaks
$a(t)$有时会有异常抖动,这是因为每走一步,手机都会震动,在曲线中增加一个高频成分。这种异常抖动被称作噪音,通过学习大量的数据,我们决定走路时的加速度频率最多在5Hz,所以我们使用一个低通IIR滤波器,来消除这些澡巾,选择$\alpha$$\beta$来消除大于5Hz的信号。
2. Slow Peaks
采样率为100时,这样的一次起伏,大约用了1.5s,显然,这对于人类来说太慢了,不能称之为一步。在学习了大量的数据后,我们决定滤掉频率小于1Hz的低频成分。还是通过一个IIR来实现,只不过这次要让$\alpha\beta$组成一个高通的滤波器。
3. Short Peaks
人在玩手机,或者打电话的时候,加速度传感器也会记录下一些加速度,在我们的$a(t)$曲线中以比较短小的波动。我们可以设置一个阈值,只有在正方向超过阈值,才会计算。
4. Bumpy Peaks
我们的计步器需要适应许多人不同的步子,在处理第一和第二种情况的过程中,我们将为走动频率设置了最大值和最小值,这就意味着,有些情况下,我们可能会多滤或者少滤。
所以尽管大多数时候我们的$a(t)$曲线已经相对平滑了,但是有时候依然会出现这种凹凸不平的情况。
当这种凹凸不平出现的时候,我们有可能会错误的在一次跳动时计算多步。我们通过一种叫做滞后的方法来解决它。滞后指的是当前系统的状态不仅与当前的输入有关,也与过去一段时间的状态有关。
我们可以这样定义,只有曲线从负方向上跌破了0,那么下一次超过阈值时,才会当做一步来计算。
Ok,经过上述四个步骤,我们得到了非常好的曲线,很接近我们当初设想的正弦曲线,让我们可以以此来记步。
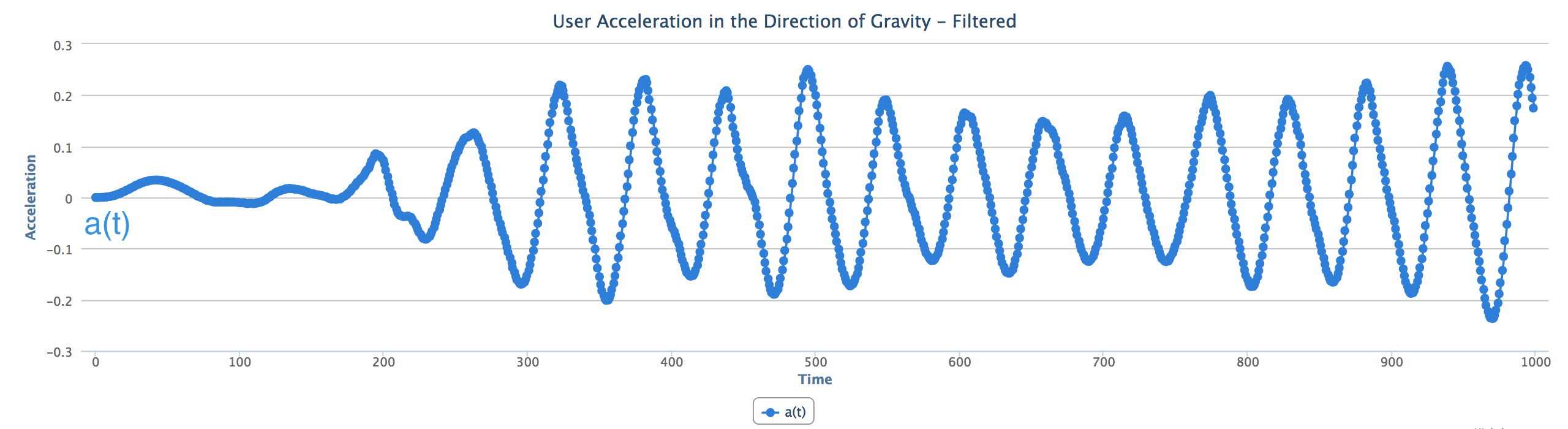
总结
记步这个问题初看起来还算直接,但是真正实现的过程中,现实世界还是出现了很多意外情况,弄的一团糟。现在让我们来回顾一下,我们是如何解决这个问题的。
- 首先我们得到总加速度
- 通过低通滤波($\leqslant 0.2Hz$)得到重力加速度
- 通过总加速度减去重力加速度得到用户加速度
- 通过点积,达到用户加速度在重力方向上的分量$a(t)$
- 针对四种情况对$a(t)$进行处理
- 针对跳动过快的波,是由于手机的意外晃动,滤去大于5Hz的波
- 针对跳动过慢的波,是由于环境的一些扰动,滤去低于1Hz的波
- 针对峰值不高的波,可能是由于打电话或者其它原因造成的,低于阈值0.1的不计数
- 针对在阈值周围抖动的波,通过设置迟滞效应,只有在波负方向经过0时,开始下一次计数。
通过数学工具,我们把复杂的问题相当的简化了,接下来,我们将开始用代码来实现这一设计。
代码实现
后面的不想翻译了,它是使用ruby加上前端代码生成的。实现的功能是上传一系列的加速度传感器的数据,系统展示过滤出来的$a(t)$,并求出步数。
以后有时间的话,我会用Java来尝试实现试试。
ruby代码的基本结果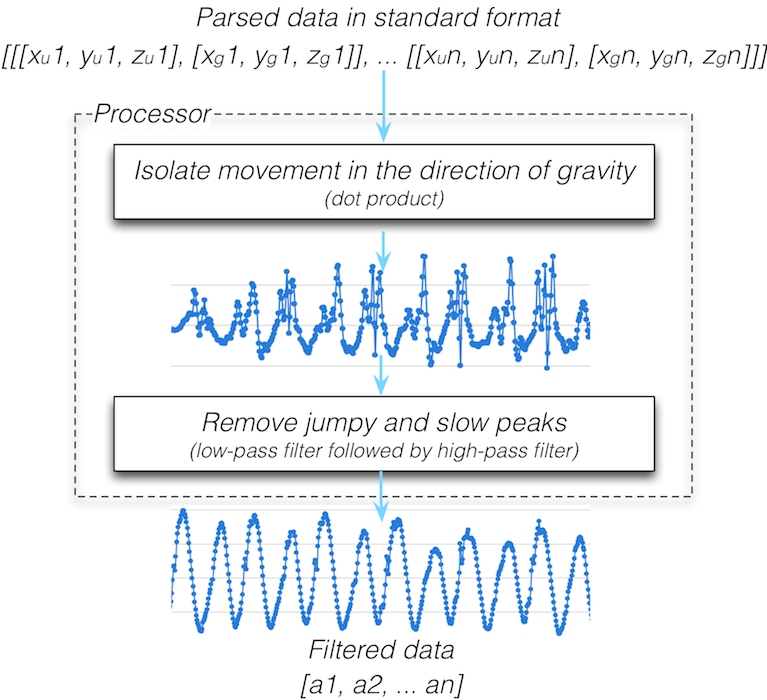
最终结果